Sonstiges Mathematik: Unterschied zwischen den Versionen

Aus DSD-Wiki
Wechseln zu: Navigation, Suche
(→‎Wordles erstellen)
(→‎Filmsequenzen zu verschiedenen Tieren:)
 
(156 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
== Materialien Integralrechnung ==
 +
[[Integralrechnung]]
 +
 +
Applet Untersumme
 +
 +
<ggb_applet width="800" height="500" filename="Holger_Untersumme.ggb" showResetIcon="true" /><br />
 +
 +
Applet Obersumme<br />
 +
<ggb_applet width="800" height="400" filename="Holger_Obersumme1.ggb" showResetIcon="true" />
 +
 +
== Materialien für trigonometrische Funkitonen ==
 +
 +
Sinus-Werte am Eineitskreis.ggb
 +
 +
<ggb_applet width="1200" height="800" filename="Sinus-Werte am Eineitskreis.ggb" showResetIcon="true" />
 +
 +
== Mathematik und Sprachlernen im Grundschulbereich ==
 +
 +
 +
=== Zootiere: Verbindung von Sprache und Mathematik ===
 +
 +
==== Arbeitsblätter: Zootiere====
 +
 +
Schon im Grundschulbereich kann man Mathematik und Sprachlernen verbinden. Dabei helfen mathematikhaltige Texte aus dem Interessenbereich der Schülerinnen und Schüler.
 +
 +
Beispielhaft werden hier Arbeitsblätter zum Thema Zootiere zur Verfügung gestellt. Die Arbeitsblätter enthalten jeweils einen einführenden Text, ein Bild, Fragen bzw. Aufgaben zum Text sowie einen Steckbrief.
 +
<br />
 +
<document>Giraffe2.pdf</document>
 +
<document>Flusspferd.pdf</document>
 +
<document>Gorilla.pdf</document>
 +
<document>Löwe.pdf</document>
 +
<document>Delfin.pdf</document>
 +
<br />
 +
Mit dem Material kann man sowohl die Kenntnisse zum Themenbereich "Größen" üben und vertiefen, als auch die Sprachkenntnisse fördern. Hinweise und methodische Anregungen für den Einsatz der Arbeitsblätter findet man im dem folgenden Beitrag von Holger Wendlandt:  <document>Mathematik_lernen_ist_auch_Sprache_lernen_BP_Sept_2010_(2).pdf</document>
 +
<br />
 +
Nachdem die SchülerInnnen mit diesen Arbeitsblättern gearbeitet haben, können sie ähnliche Materialien für weitere Tiere selbst entwickeln. Um ein jeweils gleiches Format zu gewährleisten, wird hier eine Formatvorlage bereitgestellt.
 +
*[http://wikis.zum.de/dsd/images/3/3d/Vorlage_Arbeitsblatt_Zootiere_Baja_Aug2010.doc Vorlage_Arbeitsblatt_Zootiere_Baja_Aug2010.doc]<br />
 +
 +
 +
====Filmsequenzen zu verschiedenen Tieren: ====
 +
 +
Die Filmsequenzen können als Ergänzung zu den oben angebotenen Arbeitsblättern dienen.
 +
 +
 +
 +
Wie hoch springen eigentlich Delfine?<br />
 +
{{#ev:youtube|RxRRAxJJYoU}}
 +
<br />
 +
<br />
 +
<br />
 +
Wie lang ist die Zunge einer Giraffe?<br />
 +
{{#ev:youtube|1HjsrN3MaeM}}
 +
<br />
 +
<br />
 +
<br />
 +
Was frisst ein Flusspferd?<br />
 +
{{#ev:youtube|wAxyEleFIQg}}
 +
<br />
 +
<br />
 +
<br />
 +
Wer gehört zum Löwenrudel? <br />
 +
{{#ev:youtube|jJUUJZlndys}}
 +
 +
====Informationen zu Tieren im Internet:====
 +
 +
http://www.focus.de/wissen/wissenschaft/natur/extreme-giganten-der-tierwelt_aid_535675.html
 +
 +
http://www.focus.de/wissen/wissenschaft/natur/rekorde-die-sportlichsten-tiere-der-welt_aid_535724.html
 +
 +
http://www.focus.de/wissen/wissenschaft/natur/intelligenz-die-schlauesten-tiere_aid_543469.html
 +
 +
http://www.kindernetz.de/oli/tierlexikon/
 +
 +
http://www.das-tierlexikon.de/
 +
 +
http://www.kinder-tierlexikon.de/suchliste.htm
 +
 +
 +
==Link auf die Mathe-Fachsprachenseite im DSD-Wiki==
 +
 +
*[[Benutzer:Holger|Mathe-Fachsprachenseite]]
 +
 +
<document>Vorlage_Arbeitsblatt_Zootiere_Baja_Aug2010.doc‎</document>
 +
 +
== Verschiedenes zur Mathematik ==
 +
 +
=== Zykloide mit GeoGebra ===
 +
<ggb_applet width="600" height="400" filename="Holger_Zykloide.ggb" showResetIcon="true" />
 +
 +
 +
 +
[[Zykloide]]
 +
 
=== Das Pick-Theorem===
 
=== Das Pick-Theorem===
 
In einem Gitternetz kann man den Flächeninhalt einfacher Gebiete durch Abzählen der Gitterpunkte bestimmen.
 
In einem Gitternetz kann man den Flächeninhalt einfacher Gebiete durch Abzählen der Gitterpunkte bestimmen.
Zeile 5: Zeile 98:
  
 
Hier findet man [http://www.cut-the-knot.org/ctk/PickApps.shtml Anwendungen] des Satzes (Anzahl der Gitterpunkte in einem Gebiet).
 
Hier findet man [http://www.cut-the-knot.org/ctk/PickApps.shtml Anwendungen] des Satzes (Anzahl der Gitterpunkte in einem Gebiet).
−
 
−
 
−
 
  
 
=== Gut in Mathe? ===
 
=== Gut in Mathe? ===
Zeile 27: Zeile 117:
 
Diese Einstellung wird oftmals durch ein Umfeld begünstigt, indem es "gefällig" ist, von Mathematik keine Ahnung zu haben, nach dem Motto: "keine Ahnung, wie das mit den Binomischen Formeln funktioniert - aber du siehst, aus mir ist trotzdem etwas geworden - hahaha".
 
Diese Einstellung wird oftmals durch ein Umfeld begünstigt, indem es "gefällig" ist, von Mathematik keine Ahnung zu haben, nach dem Motto: "keine Ahnung, wie das mit den Binomischen Formeln funktioniert - aber du siehst, aus mir ist trotzdem etwas geworden - hahaha".
  
−
 
+
=== Physik der Zugfahrt ===
−
 
+
http://www.youtube.com/watch?v=_FKAX25eVXE&feature=related#t=11m36s
−
=== Europäische Haupstädte ===
+
http://www.youtube.com/watch?v=_FKAX25eVXE&feature=related#t=14m09s
−
 
+
−
# Budapest
+
−
# Bukarest
+
−
# Bratislava
+
  
 
=== Eine schöne Formel ===
 
=== Eine schöne Formel ===
Zeile 44: Zeile 130:
  
  
−
<td width="100px" height="100px" style="background-color:lightblue">
 
−
<center><span class="_togglegroup _toggle_initshow _toggle _toggler toggle-visible" style="display:none;">[Anzeigen]</span><span class="_toggle_inithide _toggle _toggler toggle-hidden" style="display:none;">[Verstecken]</span>
 
−
<div class="_toggle_inithide _toggle toggle-hidden">
 
−
<span style="font-size:25pt">111</span></div></center>
 
−
</td><td width="100px" height="100px" style="background-color:lightblue">
 
−
<center><span class="_togglegroup _toggle_initshow _toggle _toggler toggle-visible" style="display:none;">[Anzeigen]</span><span class="_toggle_inithide _toggle _toggler toggle-hidden" style="display:none;">[Verstecken]</span>
 
  
−
<div class="_toggle_inithide _toggle toggle-hidden">
+
[[Bild:Quadrat_klein.JPG‎]]
−
<span style="font-size:25pt">L</span></div></center>
+
[[Bild:Quadrat_klein_Wt.jpg]]
−
</td><td width="100px" height="100px" style="background-color:lightblue">
+
 
−
<center><span class="_togglegroup _toggle_initshow _toggle _toggler toggle-visible" style="display:none;">[Anzeigen]</span><span class="_toggle_inithide _toggle _toggler toggle-hidden" style="display:none;">[Verstecken]</span>
+
===Vierecke zuordnen ===
−
<div class="_toggle_inithide _toggle toggle-hidden">
+
<div class="zuordnungs-quiz">
−
<span style="font-size:25pt">22</span></div></center>
+
 
−
</td><td width="100px" height="100px" style="background-color:lightblue">
+
{|
−
<center><span class="_togglegroup _toggle_initshow _toggle _toggler toggle-visible" style="display:none;">[Anzeigen]</span><span class="_toggle_inithide _toggle _toggler toggle-hidden" style="display:none;">[Verstecken]</span>
+
|-  
−
<div class="_toggle_inithide _toggle toggle-hidden">
+
| das Quadrat || [[Bild:Quadrat_klein.JPG‎]]
−
<span style="font-size:25pt">16</span></div></center>
+
|-  
 +
| das Trapez || [[Bild:Trapez.JPG]]
 +
|-  
 +
| die Kuh || [[Bild:Johann Friedrich Voltz Kuh.jpg|100px]]
 +
|-  
 +
| das Rechteck || [[Bild:Rechteck.JPG]]
 +
|-  
 +
| der Rhombus  || [[Bild:Romb.png]]
 +
|}
 +
 
 +
</div>
 +
 
 +
=== Primzahlen ===
 +
 
  
−
</td></tr></table></dd></dl></dd></dl></dd></dl>
 
−
<a name="Die_Primzahlen"></a><h2> <span class="mw-headline">Die Primzahlen</span></h2>
 
  
 
<dl><dt>Was sind Primzahlen?
 
<dl><dt>Was sind Primzahlen?
−
</dt><dd>Primzahlen sind Zahlen, die nur durch <b>Eins</b> und <b>sich selbst</b> teilbar sind. Also <b>T(a)={1;a}</b>
+
<dd>Primzahlen sind Zahlen, die nur durch <b>Eins</b> und <b>sich selbst</b> teilbar sind. Eine Primzahl a hat also nur <b>zwei Teiler</b>: die Eins und die Zahl selbst: Also <b>T(a)={1;a}</b>
  
−
</dd><dd>Verstanden? Na, dann kannst Du mir sicher sagen, ob diese Zahlen auch Primzahlen sind. Wenn du wissen willst, was die richtige Lösung ist, markiere das farbige Feld.  
+
<dd>Verstanden? Na, dann kannst Du mir sicher sagen, ob diese Zahlen auch Primzahlen sind. Wenn du wissen willst, was die richtige Lösung ist, markiere das farbige Feld.  
−
</dd></dl>
+
</dl>
−
<dl><dd><b>89</b>  <u style="color:red;background:red"> ist eine Primzahl.</u> 
+
−
</dd><dd><b>21</b>  <u style="color:blue;background:blue"> ist keine Primzahl.</u>
+
−
</dd><dd><b>53</b>  <u style="color:green;background:green"> ist eine Primzahl.</u>
+
  
−
</dd></dl>
+
<dl><dd><b>13</b> <u style="color:red;background:red"> ist eine Primzahl. T(13)={1;13}  .</u>
−
<div class="floatright"><span><a href="/rmg/index.php/Bild:Erathostenes.jpg" class="image" title="Erathostenes.jpg"><img alt="" src="/rmg/images/0/09/Erathostenes.jpg" width="400" height="291" border="0" /></a></span></div>
+
<dd><b>21</b>  <u style="color:blue;background:blue"> ist keine Primzahl. T(21)={1;3;7;21}.</u>
−
<dl><dd>Eine besondere Primzahl ist <i>die Zwei</i>, da sie die <i>einzige gerade Primzahl</i> ist.
+
<dd><b>29</b> <u style="color:green;background:green"> ist eine Primzahl. T(29)={1;29}  .</u>
−
</dd></dl>
+
 
 +
<dl><dd>Eine besondere Primzahl ist <i>die Zwei</i>, da sie die <i>einzige gerade Primzahl</i> ist.</dl>
 
<p><br />
 
<p><br />
 
</p>
 
</p>
−
<dl><dt>Wie man Primzahlen siebt
 
−
</dt></dl>
 
−
<dl><dd>Wenn du Schwierigkeiten mit <b>Primzahlen</b> hast, dann bist du hier genau richtig, denn ein kluger <b>alter Grieche</b>, der <b>Erathostenes</b> hieß, konnte <b>Primzahlen</b> aus dem <b>Hunderter-Raum</b> <i>"heraussieben."</i> Wie er dass gemacht hat, kann ich dir zeigen und erklären:
 
  
−
</dd><dd>Am besten lässt sich dass zeigen mit einer Hunderter-Tabelle.
 
−
</dd></dl>
 
−
<div class="floatright"><span><a href="/rmg/index.php/Bild:Lenhart_Vielf5_03.jpg" class="image" title="Lenhart Vielf5 03.jpg"><img alt="" src="/rmg/images/9/95/Lenhart_Vielf5_03.jpg" width="295" height="250" border="0" /></a></span></div>
 
−
<p><b>1.</b>
 
−
</p>
 
−
<dl><dd>Zuerst musst du die Zahlen, die durch zwei teilbar sind markieren. Dabei musst du beachten, dass die zwei sowie alle anderen Zahlen, durch die du teilst, hier eine Sonderzahl ist.
 
−
</dd></dl>
 
−
<p><b>2.</b>
 
−
</p>
 
−
<dl><dd>Nun markierst du auch die durch drei teilbaren Zahlen und gehst genauso wie bei Schritt 1 vor.
 
−
</dd></dl>
 
−
<p><b>3.</b>
 
−
</p>
 
−
<dl><dd>Du machst dasselbe wie bei den vorherigen Schritten auch bei den Zahlen aus der Vielfachenmenge von fünf(1) und sieben(2).
 
  
−
</dd></dl>
+
=== Schüttel-Quiz zum Thema: Potenzgesetze ===
−
<p><br />
+
−
</p><p>Alle nun <b>nicht markierten Zahlen</b>, bis auf die Eins, sind <b>Primzahlen.</b>
+
−
Wenn du Alles richtig gemacht hast, dann müsstest du  2, 3, 5, 7, 11, 13, 17, 19, 23, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 und 97 rausgesiebt haben. Aber Vorsicht! Die 1 selbst ist keine Primzahl!
+
−
</p>
+
−
<dl><dt>So funktioniert also das <b>Sieb des Erathostenes!</b>
+
−
</dt></dl>
+
−
<p>Und hier kannst du die Primzahlen von einem <a href="http://arndt-bruenner.de/mathe/scripts/eratosthenes.htm" class="external text" title="http://arndt-bruenner.de/mathe/scripts/eratosthenes.htm" rel="nofollow">Programm sieben lassen</a>.
+
−
</p><p><br />
+
  
−
</p><p><br />
+
<div class="schuettel-quiz">
−
</p>
+
 
 +
Die Buchstaben der fehlenden Wörter sind vertauscht. Schreibe die Wörter richtig in die Lücken
 +
Finden Sie die unverdrehte Lösung zu den verdrehten Wörtern!
 +
 
 +
Potenzen mit gleicher '''Basis''' werden multipliziert, '''indem''' man ihre Exponenten '''addiert''' und die Basis '''beibehält'''.
 +
</div>
 +
[[Bild:Rechteck.JPG‎]] </div>
 +
[[Bild:Quadrat_klein_3.jpg]]
 +
[[Bild:Rechteck.jpg]]
 +
 
 +
 
 +
 
 +
<quiz>
 +
{ Ergänze die fehlenden Präpositionen!
 +
| type="{}" }
 +
Karl: "Hallo Anne, ich bin  { im } Kino, wo bist du?"
 +
Anne: "Ich warte { vor } dem Eingang! Und wo bist du?"
 +
Karl: "Ich stehe { hinter } { dem } Eingang."
 +
Anne: "Gehen wir noch { ins } Cafe Central?"
 +
Karl: "Gern, { im } Cafe Central war ich schon lange nicht."
 +
</quiz>
 +
 
 +
 
 +
=== Hangman ===
 +
<div class="buchstabenraten-quiz">
 +
<h2 id="buchstabenraten-quiz">Buchstabenraten-Quiz</h2>
 +
<p>Erraten Sie die Wörter, indem Sie passende Buchstaben finden!</p>
 +
<p>Die Wörter haben alle mit Tieren und Insekten zu tun.</p>
 +
<table>
 +
<tr><td>Birne</td></tr>
 +
<tr><td>Biene</td></tr>
 +
 
 +
<tr><td>Ameise</td></tr>
 +
<tr><td>Pferd</td></tr>
 +
<tr><td>Käfer</td></tr>
 +
<tr><td>Schaf</td></tr>
 +
<tr><td>Schwein</td></tr>
 +
</table>
 +
 
 +
</div>
  
 
===Variablen sind wichtig ===
 
===Variablen sind wichtig ===
  
 
http://www.wordle.net/show/wrdl/1360771/Variablen
 
http://www.wordle.net/show/wrdl/1360771/Variablen
−
<check></check>
+
 
 +
 
 +
=== Volumenmessung mit der Differenzmethode ===
 +
 
 +
Fülle die Lücken richtig aus, indem du das richtige Wort mit der Maus an die richtige Stelle ziehst.
 +
 
 +
<div class="lueckentext-quiz">
 +
 
 +
1. Ich ziehe '''den ersten Messwert''' vom '''zweiten''' Messwert '''ab'''.
 +
 
 +
</div>
 +
 
 +
<div class="lueckentext-quiz">
 +
 
 +
2. Ich lese den Messwert '''für das Volumen''' des Wassers '''[mit Körper]''' ab.
 +
 
 +
</div>
 +
 
 +
<div class="lueckentext-quiz">
 +
 
 +
3. Ich tauche '''den Körper''' ins '''Wasser'''.
 +
 
 +
</div>
 +
 
 +
<div class="lueckentext-quiz">
 +
 
 +
4. Ich fülle '''das Wasser''' in das '''Messgefäß'''.
 +
</div>
 +
 
 +
<div class="lueckentext-quiz">
 +
 
 +
5. Ich lese den Messwert '''für das Volumen''' des Wassers '''[ohne Körper]''' ab.
 +
</div>
 +
 
 +
== Weitere Links ==
 +
 
 +
*Auch so kann Mathe Spaß machen: [[:zum-wiki:Mathematische Rundgänge|Mathematische Rundgänge]]
 +
*[[:zum-wiki:Mathematik-digital]] im ZUM-Wiki
 +
*[[:zum-wiki:Mathematik-digital/Flächeninhalt des Rechtecks]]
 +
 
 +
[[Kategorie:Deutschsprachiger Fachunterricht]]
 +
[[Kategorie:Mathematik]]

Aktuelle Version vom 8. April 2014, 21:02 Uhr

Inhaltsverzeichnis

Materialien Integralrechnung

Integralrechnung

Applet Untersumme


Applet Obersumme

Materialien für trigonometrische Funkitonen

Sinus-Werte am Eineitskreis.ggb

Mathematik und Sprachlernen im Grundschulbereich

Zootiere: Verbindung von Sprache und Mathematik

Arbeitsblätter: Zootiere

Schon im Grundschulbereich kann man Mathematik und Sprachlernen verbinden. Dabei helfen mathematikhaltige Texte aus dem Interessenbereich der Schülerinnen und Schüler.

Beispielhaft werden hier Arbeitsblätter zum Thema Zootiere zur Verfügung gestellt. Die Arbeitsblätter enthalten jeweils einen einführenden Text, ein Bild, Fragen bzw. Aufgaben zum Text sowie einen Steckbrief.
<document>Giraffe2.pdf</document> <document>Flusspferd.pdf</document> <document>Gorilla.pdf</document> <document>Löwe.pdf</document> <document>Delfin.pdf</document>
Mit dem Material kann man sowohl die Kenntnisse zum Themenbereich "Größen" üben und vertiefen, als auch die Sprachkenntnisse fördern. Hinweise und methodische Anregungen für den Einsatz der Arbeitsblätter findet man im dem folgenden Beitrag von Holger Wendlandt: <document>Mathematik_lernen_ist_auch_Sprache_lernen_BP_Sept_2010_(2).pdf</document>
Nachdem die SchülerInnnen mit diesen Arbeitsblättern gearbeitet haben, können sie ähnliche Materialien für weitere Tiere selbst entwickeln. Um ein jeweils gleiches Format zu gewährleisten, wird hier eine Formatvorlage bereitgestellt.


Filmsequenzen zu verschiedenen Tieren:

Die Filmsequenzen können als Ergänzung zu den oben angebotenen Arbeitsblättern dienen.


Wie hoch springen eigentlich Delfine?




Wie lang ist die Zunge einer Giraffe?




Was frisst ein Flusspferd?




Wer gehört zum Löwenrudel?

Informationen zu Tieren im Internet:

http://www.focus.de/wissen/wissenschaft/natur/extreme-giganten-der-tierwelt_aid_535675.html

http://www.focus.de/wissen/wissenschaft/natur/rekorde-die-sportlichsten-tiere-der-welt_aid_535724.html

http://www.focus.de/wissen/wissenschaft/natur/intelligenz-die-schlauesten-tiere_aid_543469.html

http://www.kindernetz.de/oli/tierlexikon/

http://www.das-tierlexikon.de/

http://www.kinder-tierlexikon.de/suchliste.htm


Link auf die Mathe-Fachsprachenseite im DSD-Wiki

<document>Vorlage_Arbeitsblatt_Zootiere_Baja_Aug2010.doc‎</document>

Verschiedenes zur Mathematik

Zykloide mit GeoGebra


Zykloide

Das Pick-Theorem

In einem Gitternetz kann man den Flächeninhalt einfacher Gebiete durch Abzählen der Gitterpunkte bestimmen.

Übersicht auf Wikipedia

Hier findet man Anwendungen des Satzes (Anzahl der Gitterpunkte in einem Gebiet).

Gut in Mathe?

Wer ist gut in Mathe? Nur ein Mathe-Genie? Prof. Manfred Spitzer gibt auf diese Frage eine interessante Antwort:

Auf die Frage, warum die Noten in Mathe nicht besonders gut sind, geben viele Schüler typische Antworten:

- für Mahte bin ich nicht begabt. - Mathe liegt mir nicht. - schon meine Mutter hatte damit in der Schule Schwierigkeiten. - mir liegen eher die Sprachen. - ioh bin eben nicht Einstein.

Der Film "Good Will Hunting" transportiert diese Haltung: Ein Professor am MIT stellt seinen Studenten eine schwere Mathematikaufgabe. Nachdem die Studenten den Hörsaal verlassen haben, geht Will, eine junge Putzkraft ohne akademische Ausbildung zur Tafel, schaut sich das Problem an, und schreibt kurzerhand die Lösung an - ein neues Mathe-Genie ist gefunden.

Diese Einstellung wird oftmals durch ein Umfeld begünstigt, indem es "gefällig" ist, von Mathematik keine Ahnung zu haben, nach dem Motto: "keine Ahnung, wie das mit den Binomischen Formeln funktioniert - aber du siehst, aus mir ist trotzdem etwas geworden - hahaha".

Physik der Zugfahrt

http://www.youtube.com/watch?v=_FKAX25eVXE&feature=related#t=11m36s http://www.youtube.com/watch?v=_FKAX25eVXE&feature=related#t=14m09s

Eine schöne Formel

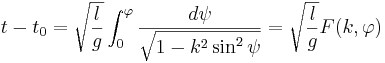
t-t_{0}=\sqrt{\frac{l}{g}}\int_{0}^{\varphi}{\frac{d\psi}{\sqrt{1-k^{2}\sin^{2} {\psi}}}} = \sqrt{\frac{l}{g}} F(k,\varphi)


Wordles erstellen

http://www.wordle.net/create


Quadrat klein.JPG Quadrat klein Wt.jpg

Vierecke zuordnen

das Quadrat Quadrat klein.JPG
das Trapez Trapez.JPG
die Kuh Johann Friedrich Voltz Kuh.jpg
das Rechteck Rechteck.JPG
der Rhombus Romb.png

Primzahlen

Was sind Primzahlen?
Primzahlen sind Zahlen, die nur durch Eins und sich selbst teilbar sind. Eine Primzahl a hat also nur zwei Teiler: die Eins und die Zahl selbst: Also T(a)={1;a}
Verstanden? Na, dann kannst Du mir sicher sagen, ob diese Zahlen auch Primzahlen sind. Wenn du wissen willst, was die richtige Lösung ist, markiere das farbige Feld.
13 ist eine Primzahl. T(13)={1;13} .
21 ist keine Primzahl. T(21)={1;3;7;21}.
29 ist eine Primzahl. T(29)={1;29} .
Eine besondere Primzahl ist die Zwei, da sie die einzige gerade Primzahl ist.



Schüttel-Quiz zum Thema: Potenzgesetze

Die Buchstaben der fehlenden Wörter sind vertauscht. Schreibe die Wörter richtig in die Lücken Finden Sie die unverdrehte Lösung zu den verdrehten Wörtern!

Potenzen mit gleicher Basis werden multipliziert, indem man ihre Exponenten addiert und die Basis beibehält.

Rechteck.JPG </div> Datei:Quadrat klein 3.jpg Rechteck.jpg


Pluspunkt für eine richtige Antwort:  
Minuspunkte für eine falsche Antwort:
Ignoriere den Fragen-Koeffizienten:

1. Ergänze die fehlenden Präpositionen!

Karl: "Hallo Anne, ich bin Kino, wo bist du?"
Anne: "Ich warte dem Eingang! Und wo bist du?"
Karl: "Ich stehe Eingang."
Anne: "Gehen wir noch Cafe Central?"
Karl: "Gern, Cafe Central war ich schon lange nicht."

Punkte: 0 / 0


Hangman

Buchstabenraten-Quiz

Erraten Sie die Wörter, indem Sie passende Buchstaben finden!

Die Wörter haben alle mit Tieren und Insekten zu tun.

Birne
Biene
Ameise
Pferd
Käfer
Schaf
Schwein

Variablen sind wichtig

http://www.wordle.net/show/wrdl/1360771/Variablen


Volumenmessung mit der Differenzmethode

Fülle die Lücken richtig aus, indem du das richtige Wort mit der Maus an die richtige Stelle ziehst.

1. Ich ziehe den ersten Messwert vom zweiten Messwert ab.

2. Ich lese den Messwert für das Volumen des Wassers [mit Körper] ab.

3. Ich tauche den Körper ins Wasser.

4. Ich fülle das Wasser in das Messgefäß.

5. Ich lese den Messwert für das Volumen des Wassers [ohne Körper] ab.

Weitere Links

Von „http://dsd.zum.de/index.php?title=Sonstiges_Mathematik&oldid=25613“