Sonstiges Mathematik: Unterschied zwischen den Versionen

Aus DSD-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: === Das Pick-Theorem=== In einem Gitternetz kann man den Flächeninhalt einfacher Gebiete durch Abzählen der Gitterpunkte bestimmen. [http://de.wikipedia.org/wiki/Sat...)
 
(→‎Wordles erstellen)
Zeile 43: Zeile 43:
 
http://www.wordle.net/create
 
http://www.wordle.net/create
  
 +
 +
<td width="100px" height="100px" style="background-color:lightblue">
 +
<center><span class="_togglegroup _toggle_initshow _toggle _toggler toggle-visible" style="display:none;">[Anzeigen]</span><span class="_toggle_inithide _toggle _toggler toggle-hidden" style="display:none;">[Verstecken]</span>
 +
<div class="_toggle_inithide _toggle toggle-hidden">
 +
<span style="font-size:25pt">111</span></div></center>
 +
</td><td width="100px" height="100px" style="background-color:lightblue">
 +
<center><span class="_togglegroup _toggle_initshow _toggle _toggler toggle-visible" style="display:none;">[Anzeigen]</span><span class="_toggle_inithide _toggle _toggler toggle-hidden" style="display:none;">[Verstecken]</span>
 +
 +
<div class="_toggle_inithide _toggle toggle-hidden">
 +
<span style="font-size:25pt">L</span></div></center>
 +
</td><td width="100px" height="100px" style="background-color:lightblue">
 +
<center><span class="_togglegroup _toggle_initshow _toggle _toggler toggle-visible" style="display:none;">[Anzeigen]</span><span class="_toggle_inithide _toggle _toggler toggle-hidden" style="display:none;">[Verstecken]</span>
 +
<div class="_toggle_inithide _toggle toggle-hidden">
 +
<span style="font-size:25pt">22</span></div></center>
 +
</td><td width="100px" height="100px" style="background-color:lightblue">
 +
<center><span class="_togglegroup _toggle_initshow _toggle _toggler toggle-visible" style="display:none;">[Anzeigen]</span><span class="_toggle_inithide _toggle _toggler toggle-hidden" style="display:none;">[Verstecken]</span>
 +
<div class="_toggle_inithide _toggle toggle-hidden">
 +
<span style="font-size:25pt">16</span></div></center>
 +
 +
</td></tr></table></dd></dl></dd></dl></dd></dl>
 +
<a name="Die_Primzahlen"></a><h2> <span class="mw-headline">Die Primzahlen</span></h2>
 +
<p>von <a href="/rmg/index.php/Benutzer:Ren%C3%A9_Appel" title="Benutzer:René Appel">René Appel</a> und <a href="/rmg/index.php/Benutzer:Julian_Lenhart" title="Benutzer:Julian Lenhart">Julian Lenhart</a>
 +
</p>
 +
<dl><dt>Was sind Primzahlen?
 +
</dt><dd>Primzahlen sind Zahlen, die nur durch <b>Eins</b> und <b>sich selbst</b> teilbar sind. Also <b>T(a)={1;a}</b>
 +
 +
</dd><dd>Verstanden? Na, dann kannst Du mir sicher sagen, ob diese Zahlen auch Primzahlen sind. Wenn du wissen willst, was die richtige Lösung ist, markiere das farbige Feld.
 +
</dd></dl>
 +
<dl><dd><b>89</b>  <u style="color:red;background:red"> ist eine Primzahl.</u> 
 +
</dd><dd><b>21</b>  <u style="color:blue;background:blue"> ist keine Primzahl.</u>
 +
</dd><dd><b>53</b>  <u style="color:green;background:green"> ist eine Primzahl.</u>
 +
 +
</dd></dl>
 +
<div class="floatright"><span><a href="/rmg/index.php/Bild:Erathostenes.jpg" class="image" title="Erathostenes.jpg"><img alt="" src="/rmg/images/0/09/Erathostenes.jpg" width="400" height="291" border="0" /></a></span></div>
 +
<dl><dd>Eine besondere Primzahl ist <i>die Zwei</i>, da sie die <i>einzige gerade Primzahl</i> ist.
 +
</dd></dl>
 +
<p><br />
 +
</p>
 +
<dl><dt>Wie man Primzahlen siebt
 +
</dt></dl>
 +
<dl><dd>Wenn du Schwierigkeiten mit <b>Primzahlen</b> hast, dann bist du hier genau richtig, denn ein kluger <b>alter Grieche</b>, der <b>Erathostenes</b> hieß, konnte <b>Primzahlen</b> aus dem <b>Hunderter-Raum</b> <i>"heraussieben."</i> Wie er dass gemacht hat, kann ich dir zeigen und erklären:
 +
 +
</dd><dd>Am besten lässt sich dass zeigen mit einer Hunderter-Tabelle.
 +
</dd></dl>
 +
<div class="floatright"><span><a href="/rmg/index.php/Bild:Lenhart_Vielf5_03.jpg" class="image" title="Lenhart Vielf5 03.jpg"><img alt="" src="/rmg/images/9/95/Lenhart_Vielf5_03.jpg" width="295" height="250" border="0" /></a></span></div>
 +
<p><b>1.</b>
 +
</p>
 +
<dl><dd>Zuerst musst du die Zahlen, die durch zwei teilbar sind markieren. Dabei musst du beachten, dass die zwei sowie alle anderen Zahlen, durch die du teilst, hier eine Sonderzahl ist.
 +
</dd></dl>
 +
<p><b>2.</b>
 +
</p>
 +
<dl><dd>Nun markierst du auch die durch drei teilbaren Zahlen und gehst genauso wie bei Schritt 1 vor.
 +
</dd></dl>
 +
<p><b>3.</b>
 +
</p>
 +
<dl><dd>Du machst dasselbe wie bei den vorherigen Schritten auch bei den Zahlen aus der Vielfachenmenge von fünf(1) und sieben(2).
 +
 +
</dd></dl>
 +
<p><br />
 +
</p><p>Alle nun <b>nicht markierten Zahlen</b>, bis auf die Eins, sind <b>Primzahlen.</b>
 +
Wenn du Alles richtig gemacht hast, dann müsstest du  2, 3, 5, 7, 11, 13, 17, 19, 23, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 und 97 rausgesiebt haben. Aber Vorsicht! Die 1 selbst ist keine Primzahl!
 +
</p>
 +
<dl><dt>So funktioniert also das <b>Sieb des Erathostenes!</b>
 +
</dt></dl>
 +
<p>Und hier kannst du die Primzahlen von einem <a href="http://arndt-bruenner.de/mathe/scripts/eratosthenes.htm" class="external text" title="http://arndt-bruenner.de/mathe/scripts/eratosthenes.htm" rel="nofollow">Programm sieben lassen</a>.
 +
</p><p><br />
 +
 +
</p><p><br />
 +
</p>
  
 
===Variablen sind wichtig ===
 
===Variablen sind wichtig ===

Version vom 10. Juni 2010, 11:55 Uhr

Inhaltsverzeichnis

Das Pick-Theorem

In einem Gitternetz kann man den Flächeninhalt einfacher Gebiete durch Abzählen der Gitterpunkte bestimmen.

Übersicht auf Wikipedia

Hier findet man Anwendungen des Satzes (Anzahl der Gitterpunkte in einem Gebiet).



Gut in Mathe?

Wer ist gut in Mathe? Nur ein Mathe-Genie? Prof. Manfred Spitzer gibt auf diese Frage eine interessante Antwort:

Auf die Frage, warum die Noten in Mathe nicht besonders gut sind, geben viele Schüler typische Antworten:

- für Mahte bin ich nicht begabt. - Mathe liegt mir nicht. - schon meine Mutter hatte damit in der Schule Schwierigkeiten. - mir liegen eher die Sprachen. - ioh bin eben nicht Einstein.

Der Film "Good Will Hunting" transportiert diese Haltung: Ein Professor am MIT stellt seinen Studenten eine schwere Mathematikaufgabe. Nachdem die Studenten den Hörsaal verlassen haben, geht Will, eine junge Putzkraft ohne akademische Ausbildung zur Tafel, schaut sich das Problem an, und schreibt kurzerhand die Lösung an - ein neues Mathe-Genie ist gefunden.

Diese Einstellung wird oftmals durch ein Umfeld begünstigt, indem es "gefällig" ist, von Mathematik keine Ahnung zu haben, nach dem Motto: "keine Ahnung, wie das mit den Binomischen Formeln funktioniert - aber du siehst, aus mir ist trotzdem etwas geworden - hahaha".


Europäische Haupstädte

  1. Budapest
  2. Bukarest
  3. Bratislava

Eine schöne Formel

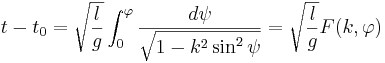
t-t_{0}=\sqrt{\frac{l}{g}}\int_{0}^{\varphi}{\frac{d\psi}{\sqrt{1-k^{2}\sin^{2} {\psi}}}} = \sqrt{\frac{l}{g}} F(k,\varphi)


Wordles erstellen

http://www.wordle.net/create


<td width="100px" height="100px" style="background-color:lightblue">

111

</td><td width="100px" height="100px" style="background-color:lightblue">

L

</td><td width="100px" height="100px" style="background-color:lightblue">

22

</td><td width="100px" height="100px" style="background-color:lightblue">

16

</td></tr></table></dd></dl></dd></dl></dd></dl>

<a name="Die_Primzahlen"></a>

Die Primzahlen

von <a href="/rmg/index.php/Benutzer:Ren%C3%A9_Appel" title="Benutzer:René Appel">René Appel</a> und <a href="/rmg/index.php/Benutzer:Julian_Lenhart" title="Benutzer:Julian Lenhart">Julian Lenhart</a>

Was sind Primzahlen?
Primzahlen sind Zahlen, die nur durch Eins und sich selbst teilbar sind. Also T(a)={1;a}
Verstanden? Na, dann kannst Du mir sicher sagen, ob diese Zahlen auch Primzahlen sind. Wenn du wissen willst, was die richtige Lösung ist, markiere das farbige Feld.
89 ist eine Primzahl.
21 ist keine Primzahl.
53 ist eine Primzahl.
<a href="/rmg/index.php/Bild:Erathostenes.jpg" class="image" title="Erathostenes.jpg"><img alt="" src="/rmg/images/0/09/Erathostenes.jpg" width="400" height="291" border="0" /></a>
Eine besondere Primzahl ist die Zwei, da sie die einzige gerade Primzahl ist.


Wie man Primzahlen siebt
Wenn du Schwierigkeiten mit Primzahlen hast, dann bist du hier genau richtig, denn ein kluger alter Grieche, der Erathostenes hieß, konnte Primzahlen aus dem Hunderter-Raum "heraussieben." Wie er dass gemacht hat, kann ich dir zeigen und erklären:
Am besten lässt sich dass zeigen mit einer Hunderter-Tabelle.
<a href="/rmg/index.php/Bild:Lenhart_Vielf5_03.jpg" class="image" title="Lenhart Vielf5 03.jpg"><img alt="" src="/rmg/images/9/95/Lenhart_Vielf5_03.jpg" width="295" height="250" border="0" /></a>

1.

Zuerst musst du die Zahlen, die durch zwei teilbar sind markieren. Dabei musst du beachten, dass die zwei sowie alle anderen Zahlen, durch die du teilst, hier eine Sonderzahl ist.

2.

Nun markierst du auch die durch drei teilbaren Zahlen und gehst genauso wie bei Schritt 1 vor.

3.

Du machst dasselbe wie bei den vorherigen Schritten auch bei den Zahlen aus der Vielfachenmenge von fünf(1) und sieben(2).


Alle nun nicht markierten Zahlen, bis auf die Eins, sind Primzahlen.

Wenn du Alles richtig gemacht hast, dann müsstest du 2, 3, 5, 7, 11, 13, 17, 19, 23, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 und 97 rausgesiebt haben. Aber Vorsicht! Die 1 selbst ist keine Primzahl!

So funktioniert also das Sieb des Erathostenes!

Und hier kannst du die Primzahlen von einem <a href="http://arndt-bruenner.de/mathe/scripts/eratosthenes.htm" class="external text" title="http://arndt-bruenner.de/mathe/scripts/eratosthenes.htm" rel="nofollow">Programm sieben lassen</a>.



Variablen sind wichtig

http://www.wordle.net/show/wrdl/1360771/Variablen <check></check>

Von „http://dsd.zum.de/index.php?title=Sonstiges_Mathematik&oldid=15269“